Narozeninový problém

Narozeninový problém je matematický jev, který tvrdí, že ve skupině 50 náhodně vybraných lidí existuje 97% šance, že minimálně dva z nich budou mít narozeniny ve stejný den. Ačkoliv se tohle zdá jako velmi zvláštní, existuje pro to jednoduché vysvětlení.

Spočítáme si to pomocí jevu opačného, kolik lidí nemá narozeniny ve stejný den.

Pro prvního člověka je 365 možností, kdy může mít narozeniny, pro druhého 364 možností, pro třetího 363 možností, a tak dále až po padesátého, kde je 316 možností. Když tohle vše vynásobíme dostaneme počet všech situací, kdy žádní dva lidé nemají narozeniny ve stejný den.

A protože počítáme pravděpodobnost, výsledek vydělíme všemi možnostmi a spočteme tak, že pravděpobnost, kdy 2 lidé z 50 nemají narozeniny ve stejný den.

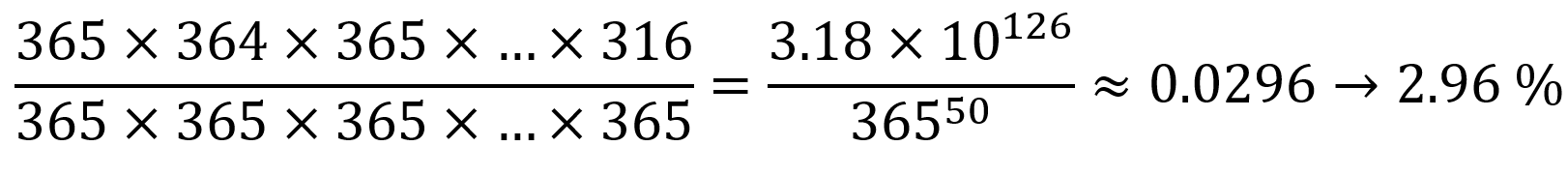
My ale chceme vědět kolik lidí má narozeniny ve stejný den, proto tuhle pravděpodobnost odečteme od 100%, čímž získáme pravděpobnost, kdy dva lidé mají narozeniny ve stejný den.

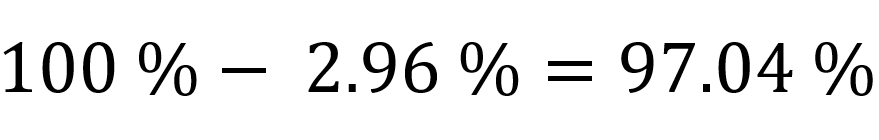
Jiný úhel pohledu

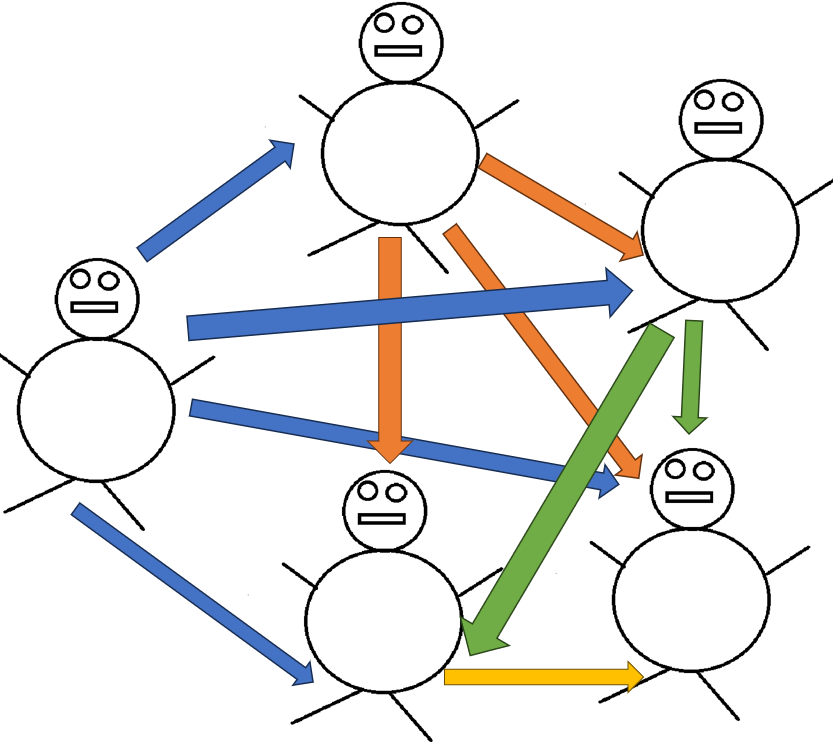
Možná to někomu stále přijde jako moc velké číslo, to je totiž dáno tím, že my nesrovnáváme jednoho člověka s ostatním 49 (modré šipky), ale každého s každým (všechny šipky), a proto dostáváme tolik možných párů.

Tabulka pravděpobností pro různě početné skupiny lidí

Pro zajímavost zde přikládám tabulku pravděpodobností pro různě velké skupiny.

Počet lidí	Pravděpobnost
2	0.27%
5	2.71%
10	11.69%
15	25.29%
20	41.14%
25	56.87%
30	70.63%
35	81.44%
40	89.12%
45	94.10%
50	97.04%
55	98.63%
60	99.41%
65	99.77%
70	99.92%

Video vysvětlení

A pokud preferujete video nad textem můžete se podívat na vysvětlení na mém Tiktoku.

@studijni_materialy #zajimavosti #birthday #foryou ♬ original sound - 𝗠𝗮𝗿𝘁𝗶𝗻 𝗛𝗲𝗷𝗽𝗲𝘁𝗿